
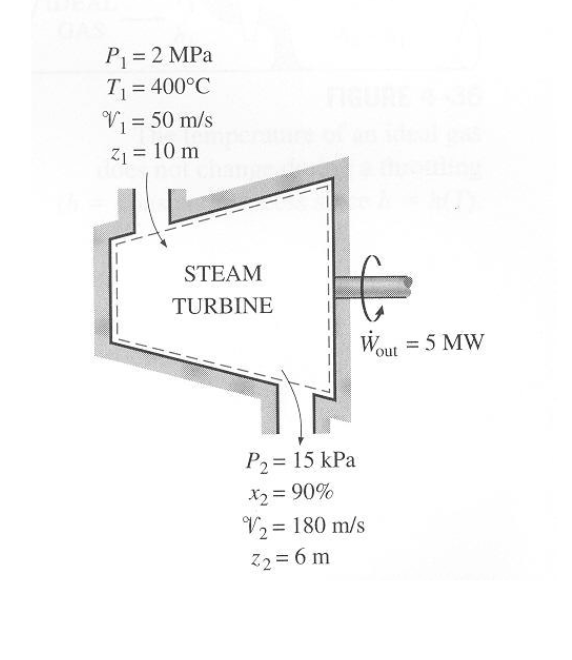
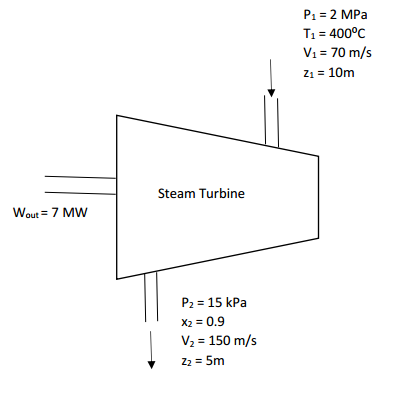
The pressure decreases at constant volume. We can now use the equation of state of an ideal gas applied to state 3:Īs expected, the temperature in state 3 is lower than in state 2, since from state 2 to state 3 And we can determine it by applying the equation of state of an ideal gas to state 1: But first we need to determine the number of moles in the sample of ideal gas. We can use the equation of state of an ideal gas applied to state 3 to calculate the temperature. Where we have expressed the pressure in pascals using the following conversion: Pressure and volume in state 1 are knowns on the other hand, the volumes in states 3 and 2 are the same (see the thermodynamic cycle in the PV diagram), so we can use the adiabatic process equation to calculate the pressure in state 3: Where γ is the heat capacity ratio (or adiabatic index), that in the case of a monatomic ideal gas is given by: The equation for an adiabatic process expressed as a function of pressure and volume is: The thermodynamic cycle undergone by the ideal gas is represented in the next figure: We recommend you to give a look at the reversible processes of an ideal gas page before trying to solve it. This problem is an application of the first law of Thermodynamics. Calculate the energy transfers for each stage. Assuming a flow rate of 1 kg/s throughout determine the condition and specific enthalpy at each point in the cycle. As a result of the compression, the wet steam is changed completely into saturated water. Please consider supporting us by disabling your ad blocker on YouPhysics. The exhaust steam is partially condensed and then compressed back to 10 bar.


 0 kommentar(er)
0 kommentar(er)
